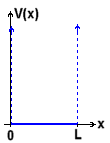
Grundlagen der QM - Eigenfunktionen und Eigenwerte (Beispiel) Mit der stationären Schrödingergleichung lassen sich die Wellenfunktionen Y n (x) für stationäre Zustände berechnen. Ein quantenmechanisches Problem besitzt im allgemeinen mehrere stationäre Lösungen.  Betrachten wir als Beispiel ein Teilchen, dass sich nur eindimensional zwischen einem Ort 0 und dem Ort L befinden darf. Man spricht in diesem Fall von einem eindimensionalen, unendlich hohen Potenzial-"Topf" der Länge L, in dem das Teilchen eingeschlossen ist ( Randbedingungen : V = 0 im Potenzialtopf; außerhalb: V = ¥ ). Das unendlich große Potenzial außerhalb des Topfs stellt eine unüberwindliche Hürde für das Teilchen dar. Als Lösung der stationären Schrödingergleichung erhält man nicht nur eine, sondern mehrere Lösungen, die sich alle durch eine Quantenzahl (hier: n = {1, 2, 3, ...}) unterscheiden. Verschiedene Lösungen Y n (x) der stationären Schrödingergleichung eines quantenmechanischen Problems (z.B. Wasserstoffatom) nennt man Energie-Eigenfunktionen Y n (x) .  Was kann man sich unter einer Eigenfunktion Y n (x) vorstellen? Anschaulich kann man die Eigenfunktionen eines Teilchens im unendlich hohen Potenzialtopf mit den Eigenschwingungen einer eingespannten Saite vergleichen. Das Teilchen befindet sich zwischen Grenzen, die es nicht überschreiten darf. Seine Eigenfunktionen müssen außerhalb dieser Grenzen " = 0 " sein. Analog dazu schwingt die Saite nur zwischen ihrem Anfangs- und Endpunkt auf der Gitarre.  Betrachtet man die schwingende Saite von der Seite, sieht man sie als eine stehende Welle mit mehr oder weniger vielen Schwingungsbäuchen. Die Anzahl der Schwingungsbäuche, deren Abstand die halbe Wellenlänge darstellt, hängt von der Art der Anregung der Saite ab. Die Wellenform der schwingenden Saite kann man als Funktionsgraph der beschreibenden Funktion interpretieren. Da es verschiedene Schwingungsformen (d.h. Eigenschwingungen) gibt, gibt es auch verschiedene Eigenfunktionen für ein und dieselbe Saite.  Auf unser Teilchen im Potenzialtopf übertragen sind diese, die Eigenschwingungen beschreibenden Funktionen, einfach die verschiedenen Eigenfunktionen der stationären Zustände. Jede Schwingung besitzt Schwingungsenergie. Verschiedene Schwingungen besitzen verschieden viel Energie. Daher besitzen auch die verschiedenen stationären Zustände, die durch die Eigenfunktionen Y n (x) beschrieben werden, mehrere bestimmte Energiewerte.  Den Energiewert des Zustands, der durch die Eigenfunktion Y n (x) beschrieben wird, nennt man Energieeigenwert E n .   Y n (x) ist daher die Energie-Eigenfunktion. Der Zustand mit der kleinsten Quantenzahl n ( n = 1 ) besitzt die kleinste Energie. Man nennt ihn daher auch den Grundzustand. Beispiel:  Die Energieeigenwerte E n des eindimensionalen, unendlich hohen Potenzialtopfs lauten: E n = n 2 . h 2 / (8mL 2 ) Grundzustand ( n = 1 ): E 1 = 1 . h 2 /(8mL 2 )  angeregter Zustand ( n = 2 ): E 2 = 4 . h 2 /(8mL 2 )    usw. ... Es gibt also nur Energieeigenwerte, die Vielfache von h 2 /(8mL 2 ) , dem Energieeigenwert des Grundzustands sind. Auf Grund dieser " Portionierung " oder " Quantelung " der Energien nennt man n eine Quanten-Zahl. Die Energieeigenwerte eines stationären Zustands sind messbar!  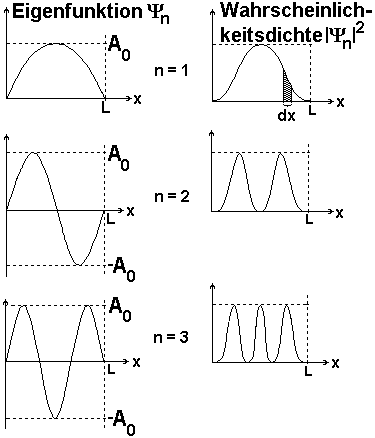Die Eigenfunktionen lauten:  Y n (x) = A 0 sin(n p x/L)   Die Eigenfunktionen erhält man aus der Schrödingergleichung und den Randbedingungen. Aus ihnen folgen die Energieeigenwerte.  Man erkennt, dass die Graphen der Eigenfunktionen sinusförmig sind und die Amplitude A 0 haben. Die Abbildung rechts oben zeigt die Eigenfunktionen der ersten drei Zustände (n = 1, 2, 3). Zusätzlich zu den Eigenfunktionen ist rechts die Wahrscheinlichkeitsdichte | Y n (x)| 2 aufgetragen. Der Inhalt der Fläche unter dem Graphen über der Strecke dx ist die Wahrscheinlichkeit dafür, dass sich das Teilchen in dx befindet. Im Grundzustand (n = 1) ist das Teilchen somit vor allem um die Mitte des Potenzialtopfs "lokalisiert". Die Wahrscheinlichkeitsdichte | Y n (x)| 2 nimmt dort ihre höchsten Werte an. In der klassischen Physik würde man ein Teilchen im Potenzialtopf zu einem festen Zeitpunkt t 1 an einem festen Ort x 1 erwarten. Das entspricht aber nicht der Realität. Diese wird hier durch die Quantenmechanik mit der Wellen- funktion völlig richtig beschrieben!  Ein Beispiel eines "Abbildes" eines stationären Zustands zeigt die Abb. rechts. Hier ist ein Elektron in einem Potenzial-"Topf" (im wahrsten Sinne des Wortes) aus 48 ringförmig angeordneten Eisenatomen eingesperrt. Die Aufnahme wurde Zeile für Zeile " gescannt ". Da das Scannen längere Zeit in Anspruch genommen hat und das Bild eine Welle darstellt, muss es sich um einen stationären Zustand des Elektrons handeln. Würde sich die Form mit der Zeit ändern, wäre kein so scharfes Wellenbild zu sehen. Die Welle stellt im Prinzip die Wahrscheinlichkeitsdichte | Y n (x)| 2 des einen Elektrons im Potenzialtopf dar. Der Potenzialtopf dieses Beispiels hat eine endliche Höhe, wobei man nicht vergessen darf, dass mit "Höhe" die Energie gemeint ist, die ein Teilchen zur sicheren Überwindung des Walls benötigt und nicht etwa die Höhe der dargestellten "Hügel"! Abb.: D.M. Eigler, IBM, Almaden-Forschungszentrum; Zitat: "We can build a box, put an electron in the box, an we see how the electrons solve the Schrödinger equation..." Nach In der Quantenmechanik hat nicht nur die Energie, sondern auch der Impuls und der Drehimpuls Eigenwerte.